Income inequality at UCSD economics, 2023

The compensation at University of California has just published the figures for 2023. I have updated the data set for my paper and run regressions. In case readers are interested in predicting their salaries, the prediction equation in 2023 is \[\log y = 12.12 -0.0100T + 0.0052N_\textrm{pub} + 0.0204N_\textrm{top5} + 0.2485D_\textrm{assoc} + 0.5048D_\text{full}, \] where \(y\) is the 9-month salary, \(T\) is the number of years elapsed since obtaining Ph.D., \(N_\textrm{pub}\) is the cumulative number of peer-reviewed research articles, \(N_\textrm{top5}\) is the cumulative number of top 5 publications, and \(D_\textrm{assoc}, D_\textrm{full}\) are dummy variables for associate and full professors.

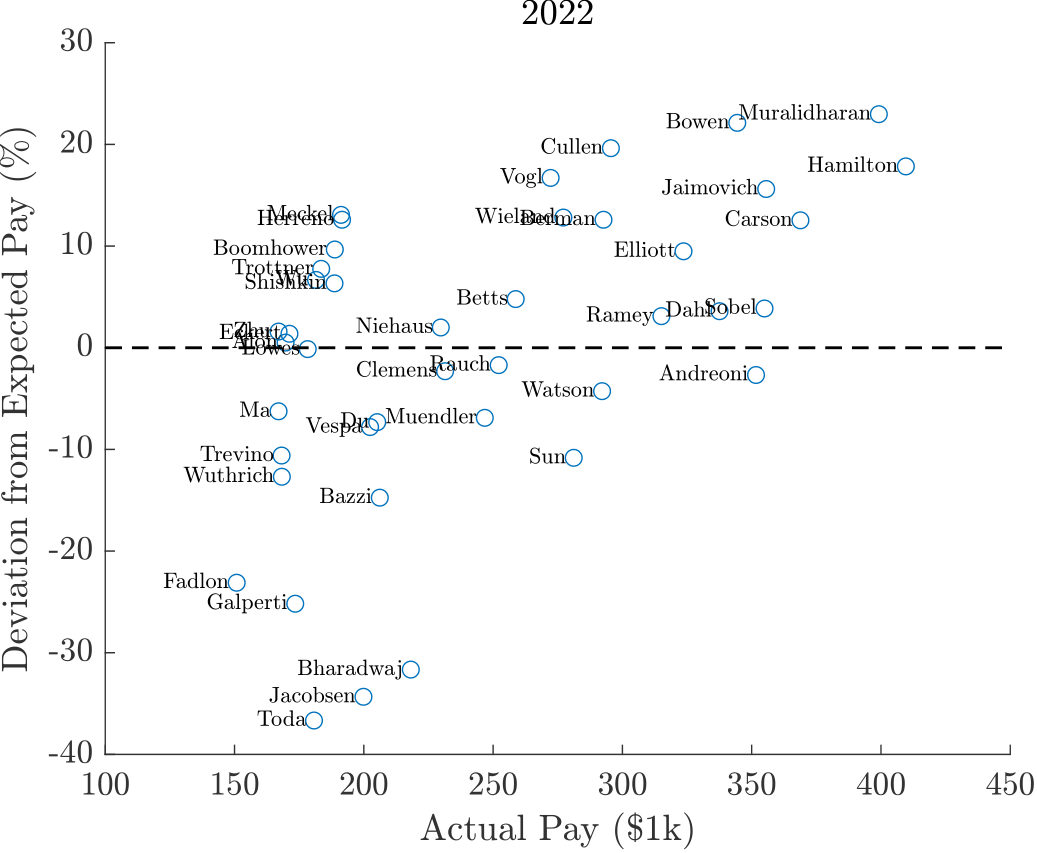
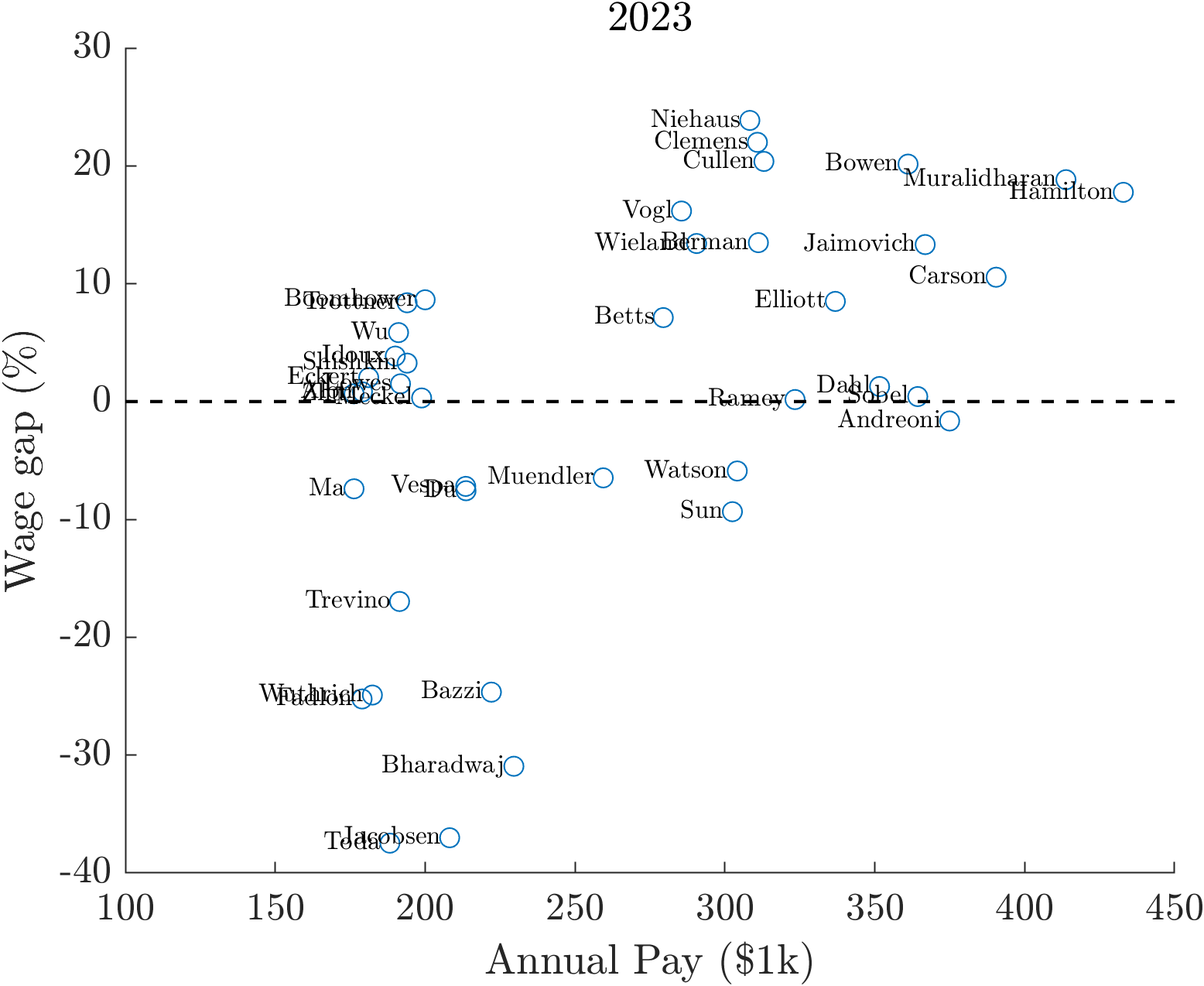
For comparison, I present both the 2022 and 2023 scatter plots. Congratulations to Jeff Clemens and Paul Niehaus for the big raise.