Radii of the Inscribed and Escribed Spheres of a Simplex

In the picture below, \(A_1A_2A_3\) is a triangle, \(I_0\) is the center of the inscribed circle with radius \(r_0\), and \(I_1,I_2,I_3\) are the centers of the escribed circles with radii \(r_1,r_2,r_3\). It is known that \[ \frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}=\frac{1}{r_0}. \] This equation appears as (24) in Mackay (1893), who attributes to Steiner and Bobillier in 1828.

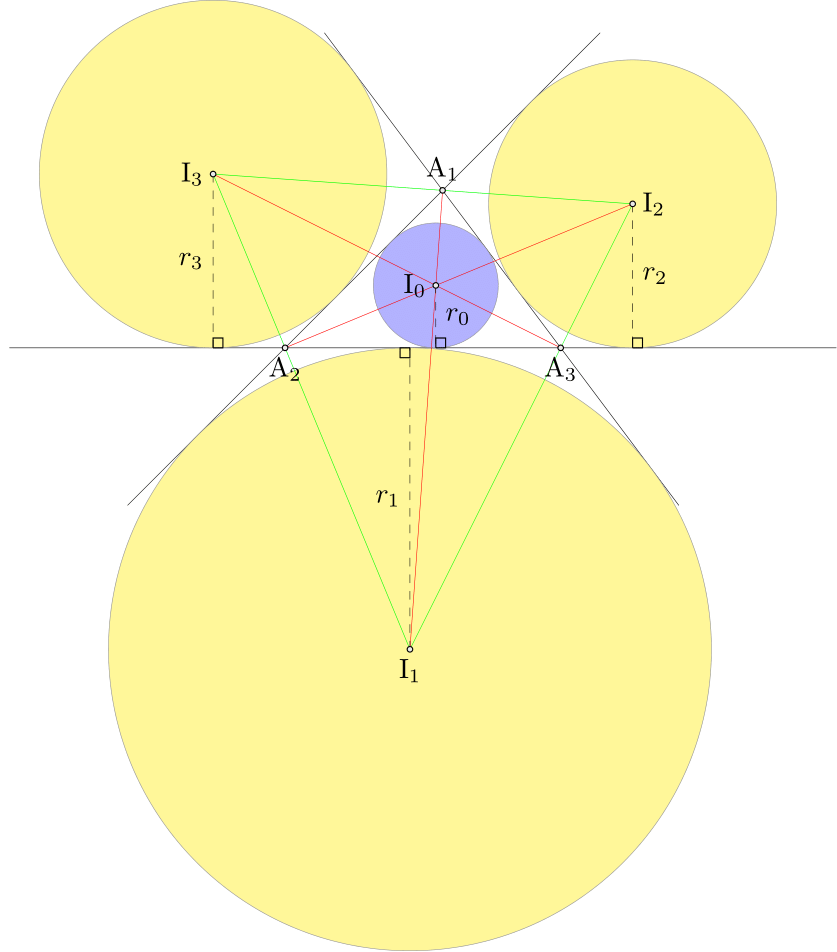
When I attended middle and high schools in the 1990s, I was fascinated by elementary geometry. I recall I discovered the above relation in 1997. In 1998, when I was a freshman at University of Tokyo, I found the three-dimensional generalization \[ \frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}+\frac{1}{r_4}=\frac{2}{r_0}, \] where \(r_0\) is the radius of the inscribed sphere of a tetrahedron and \(r_1,r_2,r_3,r_4\) are the radii of the four escribed spheres. Based on some geometric intuition I conjectured that in the \(n\)-dimensional Euclidean space, the relation \[ \sum_{k=1}^{n+1}\frac{1}{r_k}=\frac{n-1}{r_0} \] would hold. After studying linear algebra in 1999, I proved this analytically.

In those days I didn’t know how to publish papers, so my notes became dormant. After learning how to write papers and obtaining an academic job in 2013, I managed to publish it.