👍On the Emergence of a Power Law in the Distribution of COVID-19 Cases
Published in Physica D: Nonlinear Phenomena, 2020
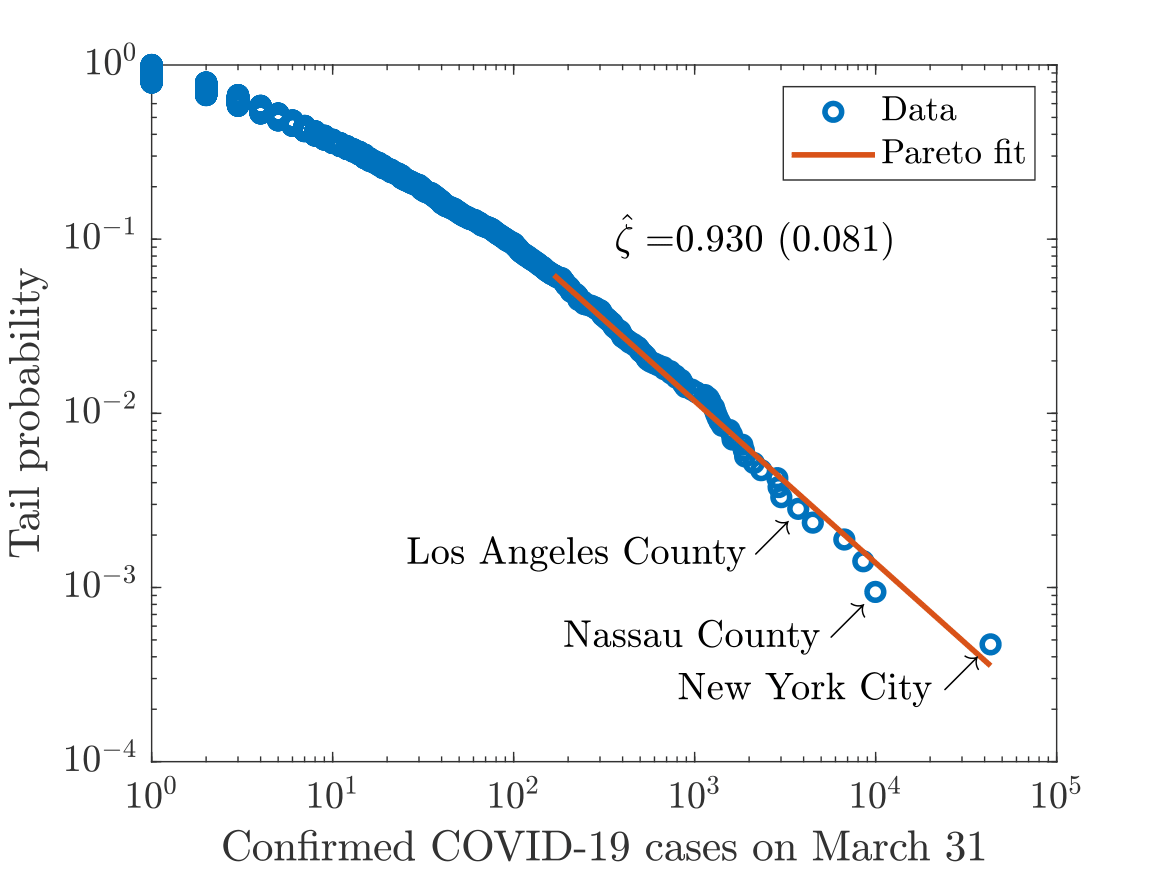
In March 2020, I was working on my paper estimating the SIR model and obtained daily data on COVID-19 cases. I was naturally interested in the size distribution of COVID cases, and not surprisingly, it obeyed the power law. But what is cool about the COVID dataset is that it is a panel data that is updated daily. Because Brendan and I had been working on the generative mechanism of power laws based on random multiplicative growth and the distribution of age (for COVID, the number of days elapsed since the first case in the particular location), it was an ideal dataset to test the theory. The empirical Pareto exponent estimated from the cross-sectional data, \(\hat{\zeta}=0.930\), and the theoretical Pareto exponent implied by the random growth mechanism, \(\zeta=0.928\), are nearly identical.
Although the paper is simple and short, I consider it one of the best papers I have written. As far as I am aware, this is the only paper that provides direct evidence for random multiplicative growth as a generative mechanism of power laws.